Please enter the following details
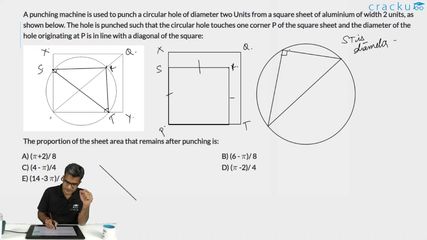
A punching machine is used to punch a circular hole of diameter two Units from a square sheet of aluminium of width 2 units, as shown below. The hole is punched such that the circular hole touches one corner P of the square sheet and the diameter of the hole originating at P is in line with a diagonal of the square:
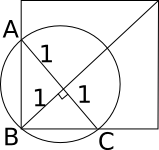
The area of triangle ABC is 1/2 * $$\sqrt2$$ * $$\sqrt2$$ = 1
Area of semi-circle ABC = $$\pi/2$$
So, area of circle outside the square = $$\pi/2$$ - 1 = ($$\pi$$ -2)/2
So, area of circle inside the sheet = $$\pi$$ - ($$\pi/2$$ - 1) = 1 + $$\pi/2$$
Area of original square = 2*2 = 4
So, area of the sheet after punching = 4 - 1 - $$\pi/2$$ = 3 - $$\pi/2$$
So, proportion of sheet that remains after punching = (3 - $$\pi/2$$)/4 = (6 - $$\pi$$)/8
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 35+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
