A square ABCD is inscribed in a circle of unit radius. Semicircles are described on each side of a diameter. The area of the region bounded by the four semicircles and the circle is
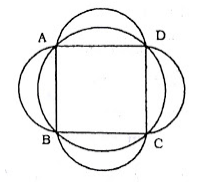
Radius of the circle = 1 unit, => Diameter = BD = 2 units
Thus, side of square = AB = $$\sqrt2$$ units
Radius of a semi-circle = $$\frac{AB}{2}=\frac{\sqrt2}{2}=\frac{1}{\sqrt2}$$
=> Area of 4 semi-circles = $$2\pi r^2$$
= $$2\pi (\frac{1}{\sqrt2})^2=\pi$$ sq. units ------------(i)
Area bounded by region = Area of circle - Area of square
= $$\pi(1)^2-(\sqrt2)^2=(\pi-2)$$ sq. units ---------------(ii)
$$\therefore$$ Required area bounded by 4 semi circles = (i) - (ii)
= $$\pi - (\pi-2) = 2$$ sq. units
=> Ans - (B)
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free

