The value of the integral $$\int_{-\frac{1}{\sqrt{3}}}^{\frac{1}{\sqrt{3}}} (\frac{x^2 - \tan x}{1 + x^2})dx$$ is equal to
$$\int_{-\frac{1}{\sqrt{3}}}^{\frac{1}{\sqrt{3}}} (\frac{x^2 - \tan x}{1 + x^2})dx$$
=$$\int_{-1/\sqrt{3}}^{1/\sqrt{3}} \frac{x^2+1-1 - \tan x}{1 + x^2}dx$$
=$$\int_{-1/\sqrt{3}}^{1/\sqrt{3}} \frac{x^2+1-1 - \tan x}{1 + x^2}dx$$
=$$\int_{-1/\sqrt{3}}^{1/\sqrt{3}}1-\int_{-1/\sqrt{3}}^{1/\sqrt{3}}\frac{1}{1+x^{2}}+\int_{-1/\sqrt{3}}^{1/\sqrt{3}}\frac{\tan x}{1+x^{2}}$$
=x-$$\tan^{-1}x$$+0 [$$\because$$
$$\frac{\tan x}{1+x^2}\ is\ an\ odd\ function,\ and\ will\ become\ zero$$
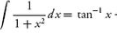
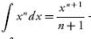
=$$\frac{1}{\sqrt{3}}-\frac{\pi}{6}$$ - $$\frac{-1}{\sqrt{3}}-\frac{\pi}{6}$$
=$$2(\frac{1}{\sqrt{3}} - \frac{\pi}{6})$$
Hence A is the correct answer.
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 40+ previous papers with solutions PDF
- Top 500 MBA exam Solved Questions for Free




