A ladder of 7.6 m long is standing against a wall and the distance between the wall and the base of the a ladder is 6.4 m. If the top of the ladder now slips by 1.2m, then the foot of the ladder shifts by approximately:
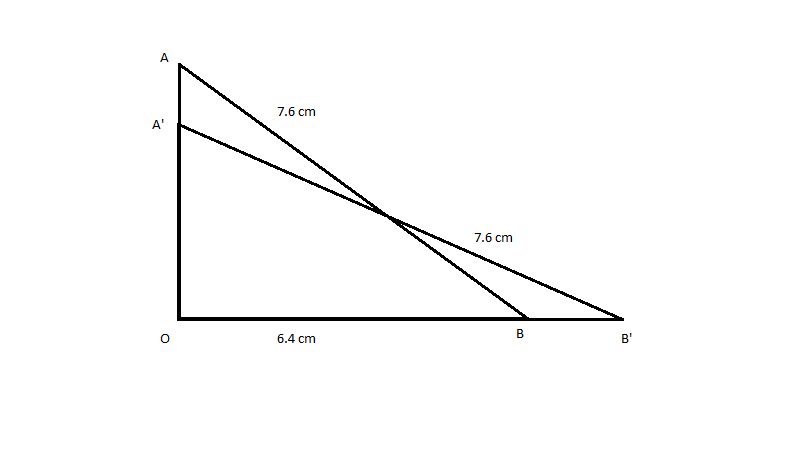
The starting position of ladder is AB.
AB = 7.6 cm and OB = 6.4 cm
Applying Pythagoras Theorem in $$\triangle$$ AOB
$$OA^{2}$$ + $$OB^{2}$$ = $$AB^{2}$$
OA = 4.10 cm
Now ladder top slips by 1.2 cm, the new position of ladder becomes A'B'
OA' = 4.10 - 1.2 = 2.9 cm
Applying Pythagoras Theorem in $$\triangle$$ A'OB'
$$OA'^{2}$$ + $$OB'^{2}$$ = $$A'B'^{2}$$
OB' = 7.02 cm
Hence, the foot of the ladder is shifted by approximately OB' - OB = 0.6cm
Video Solution

Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 170+ previous papers with solutions PDF
- Top 5000+ MBA exam Solved Questions for Free




