Suppose the length of each side of a regular hexagon ABCDEF is 2 cm.It T is the mid point of CD,then the length of AT, in cm, is
Since a regular hexagon can be considered to be made up of 6 equilateral triangles, a line joining the farthest vertices of a hexagon can be considered to be made up using the sides of two opposite equilateral triangle forming the hexagon. Hence, its length should be twice the side of the hexagon, in this case, 4 cm.
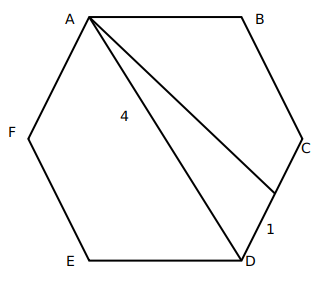
Now, AD divided the hexagon into two symmetrical halves. Hence, AD bisects angle D, and hence, angle ADC is $$60^{\circ\ }$$.
We can find out the value of AT using cosine formula:
$$AT^2=\ 4^2+1^2-2\times\ 1\times\ 4\cos60$$
$$AT^2=\ 17-4=13$$
$$AT=\sqrt{\ 13}$$
Video Solution

Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free




