Question 5

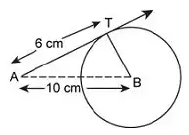
For the circle shown below, find the length (in cm) of the largest cord of the circle.

Solution

Given : AT is tangent on the circle. AT = 6 cm and AB = 10 cm

To find : Largest chord = Diameter = ?

Solution : In right $$\triangle$$ ABT

=> $$(BT)^2=(AB)^2-(AT)^2$$

=> $$(BT)^2=(10)^2-(6)^2$$

=> $$(BT)^2=100-36=64$$

=> $$BT=\sqrt{64}=8$$ cm

$$\therefore$$ Diameter = $$2\times8=16$$ cm

=> Ans - (C)

Share on Whatsapp Share on Whatsapp

Create a FREE account and get: