A function f maps the set of natural numbers to whole numbers, such that f(xy) = f(x)f(y) + f(x) + f(y) for all x, y and f(p) = 1 for every prime number p. Then, the value of f(160000) is
Looking at the additional information about the prime numbers should make one realise that they are the key to solving the question.
f(16000) can be written as $$f\left(2^8\times\ 5^4\right)$$
Now, we can try to find these individual values:
For any prime p: f(p)=1
$$f\left(p^2\right)=f\left(p\right)f\left(p\right)+f\left(p\right)+f\left(p\right)=1+1+1=3$$
$$f\left(p^3\right)=f\left(p^2\right)f\left(p\right)+f\left(p^2\right)+f\left(p\right)=3+3+1=7$$
This way, we can find the function output for any prime number raised to a power.
We can see that each new exponent is twice the previous output +1, solving this way till prime raised to power 8
$$f\left(p^4\right)=7+7+1=15$$
$$f\left(p^5\right)=15+15+1=31$$
$$f\left(p^6\right)=31+31+1=63$$
$$f\left(p^7\right)=63+63+1=127$$
$$f\left(p^8\right)=127+127+1=255$$
Using these values in the original expression of $$f\left(2^8\times\ 5^4\right)=f\left(2^8\right)f\left(5^4\right)+f\left(2^8\right)+f\left(5^4\right)$$ we get
$$f\left(2^8\times\ 5^4\right)=\left(255\times\ 15\right)+255+15=4095$$
Therefore, Option A is the correct answer.
Video Solution
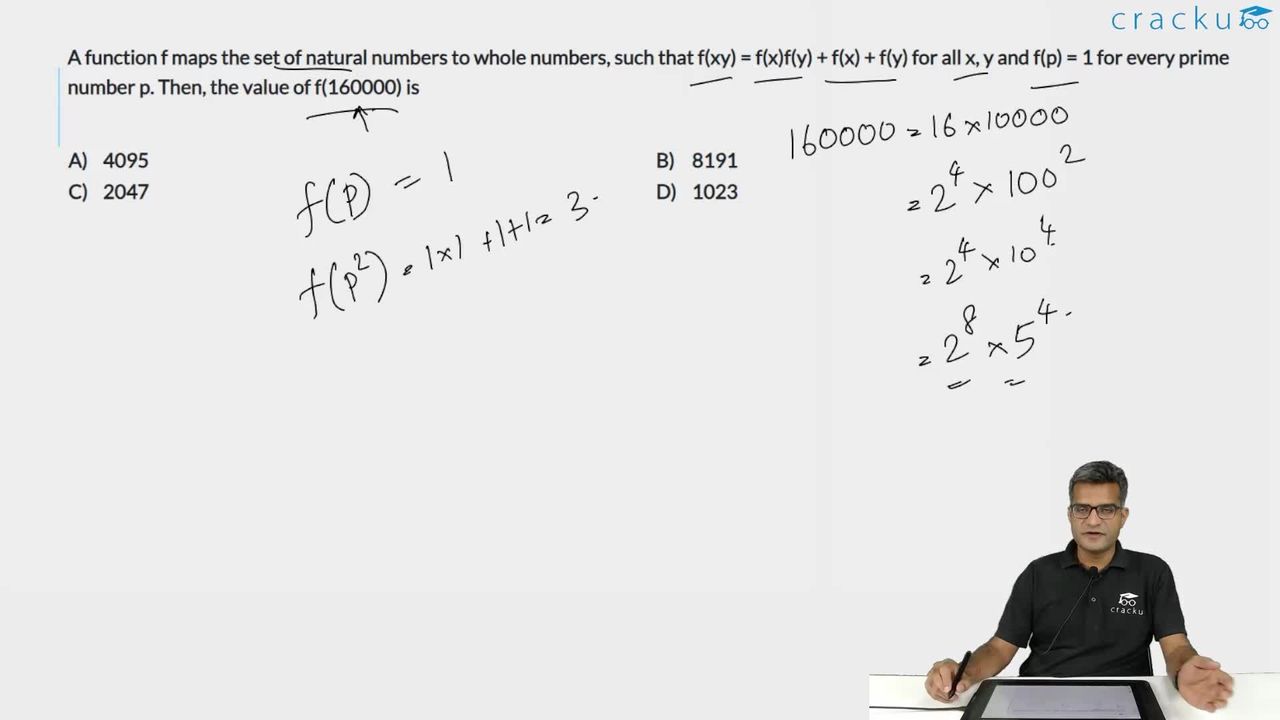
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free



