Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located 3 meters east of O. Then, the length of PQ, in meters, is nearest to
We can form the following figure based on the given information:
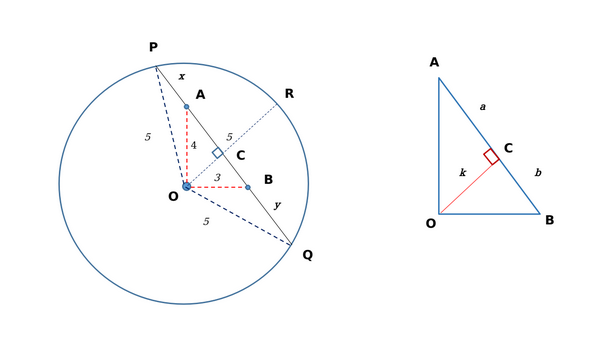
Since OA = 4 m and OB=3 m; AB = 5 m. OR bisects the chord into PC and QC.
Since AB = 5 m, we have $$a+b = 5 ...(i)$$ Also, $$4^2\ -k^2=a^2...\left(ii\right)$$ and $$3^2\ -k^2=b^2...\left(iii\right)$$
Subtracting (iii) from (ii), we get: $$a^2\ -b^2=7...\left(iv\right)$$
Substituting (i) in (iv), we get $$a - b = 1.4 ...(v)$$; $$\left[\left(a+b\right)\left(a\ -b\right)=7;\ \therefore\ \left(a-b\right)=\frac{7}{5}\right]$$
Solving (i) and (v), we obtain the value of $$a=3.2$$ and $$b=1.8$$
Hence, $$k^2\ =\ 5.76$$
Moving on to the larger triangle $$\triangle\ POC$$, we have $$5^2-k^2=\left(x+a\right)^2$$;
Substituting the previous values, we get: $$(25-5.76)=\left(x+3.2\right)^2$$
$$\sqrt{19.24}=\left(x+3.2\right)$$ or $$x = 1.19 m$$
Similarly, solving for y using $$\triangle\ QOC$$, we get $$y=2.59 m$$
Therefore, $$PQ = 5+2.59+1.19 = 8.78 \approx\ 8.8 m$$
Hence, Option A is the correct answer.
Video Solution

Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free




