Question 58

If D is the midpoint of side BC of a triangle ABC and AD is the perpendicular to AC then:

Solution

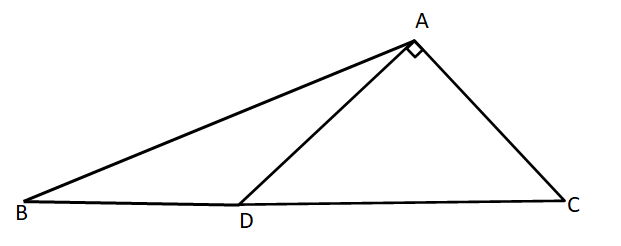
Using Apollonius theorem in $$\triangle$$ ABC, we can say that,

$$2(AD^2+BD^2) = AB^2+AC^2$$ ... (1)

In right-angle triangle ADC, $$DC^2 = AD^2 + AC^2$$ ... (2)

By equation (1) and (2), we can say that

$$2(DC^2 - AC^2 +BD^2) = AB^2+AC^2$$

$$3AC^2 = BC^2 - AB^2$$

Therefore, option A is the correct answer.

Share on Whatsapp Share on Whatsapp

Create a FREE account and get: