Question 59
If a triangle ABC, $$\angle BCA=50^{0}$$. D and E are points on $$AB$$ and $$AC$$, respectively, such that $$AD=DE$$. If F is a point on $$BC$$ such that $$BD=DF$$, then $$\angle FDE$$, in degrees, is equal to
Solution
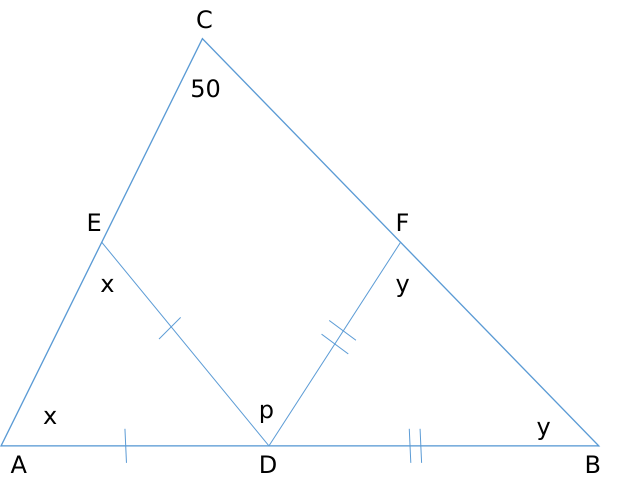

We need to find out p.
Angle ADE = 180 - 2x
Angle BDF = 180 - 2y
Now, 180 - 2y + p + 180 - 2x = 180 [Straight line = 180 deg]
p = 2x + 2y - 180
Also, x + y + 50 = 180 [Sum of the angles of triangle = 180]
x + y = 130
p = 260 - 180 = 80 degrees.
Video Solution

Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
CAT Quant Questions | CAT Quantitative Ability
CAT Averages, Ratio and Proportion QuestionsCAT Mensuration QuestionsCAT Number Systems QuestionsCAT Arithmetic QuestionsCAT Functions, Graphs and Statistics Questions
CAT DILR Questions | LRDI Questions For CAT
CAT DI with connected data sets QuestionsCAT Selection With Condition QuestionsCAT Venn Diagrams QuestionsCAT Coins and Weights QuestionsCAT Truth Lie Concept Questions




