Consider the two equiangular triangles ABC and DEF having medians as AL and DM respectively as shown in figure below.
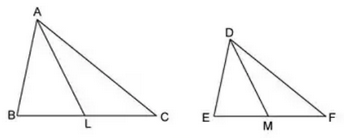 Choose the correct option for the above situation.
Choose the correct option for the above situation.It is given that $$\triangle$$ ABC and $$\triangle$$ DEF are equiangular triangles, thus corresponding angles are equal.
=> $$\triangle$$ ABC $$\sim\triangle$$ DEF
=> Ratio of perimeter = $$\frac{AB}{DE}=$$ $$\frac{BC}{EF}=$$ $$\frac{AC}{DF}$$ -------------(i)
Since, AL and DM are medians, => Ratio of perimeter of $$\triangle$$ ABC to $$\triangle$$ DEF = $$\frac{AL}{DM}$$ -----------(ii)
From, equations (i) and (ii), we get :
=> $$\frac{BC}{EF}=\frac{AL}{DM}$$
=> Ans - (B)
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free

