If the ratio of the angle bisector segments of the two equiangular triangles are in the ratio of 3:2 then what is the ratio of the corresponding sides of the two triangles?

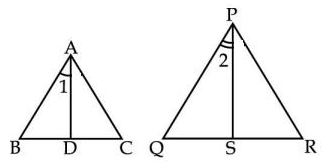
Given : $$AD:PS=3:2$$

To find : $$AB : PQ=?$$

Solution : The given triangles are equiangular, i.e. $$\angle$$ A = $$\angle$$ P , $$\angle$$ B = $$\angle$$ Q , $$\angle$$ C = $$\angle$$ R

Now, in $$\triangle$$ ABD and $$\triangle$$ PQS,

$$\angle$$ B = $$\angle$$ Q

$$\angle$$ BAD = $$\angle$$ QPS     [$$\because$$ $$\angle$$ A = $$\angle$$ P => $$\frac{1}{2}$$ $$\angle$$ A = $$\frac{1}{2}$$ $$\angle$$ P => $$\angle$$ BAD = $$\angle$$ QPS]

So, by A-A criterion of similarity, we have :

$$\triangle$$ ABD $$\sim$$ $$\triangle$$ PQS

=> $$\frac{AB}{PQ}=\frac{AD}{PS}=\frac{3}{2}$$

=> Ans - (B)