What will be the value of the angle (in degrees) subtended by the chord in the minor segment of the circle, if the length of a chord is equal to the radius of the circle?

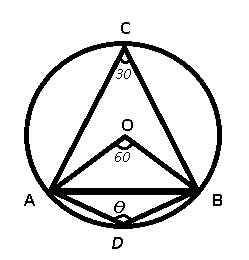
Given : Radius and the chord of the circle are equal in length.

To find : $$\angle$$ ADB = $$\theta$$ = ?

Solution : It is given that the radius and the chord of the circle are equal in length.

=> OA = OB = AB

=> AOB is an equilateral triangle, => $$\angle$$ AOB = $$60^\circ$$

Now, the angle subtended by an arc at the centre is double the angle subtended by it at any point on the circle.

=> $$\angle$$ ACB = $$\frac{60}{2}=30^\circ$$

Quadrilateral ADBC is a cyclic quadrilateral where sum of opposite angles = $$180^\circ$$

=> $$\angle$$ ACB + $$\angle$$ ADB = $$180^\circ$$

=> $$30^\circ+\theta=180^\circ$$

=> $$\theta=180^\circ-30^\circ=150^\circ$$

=> Ans - (B)