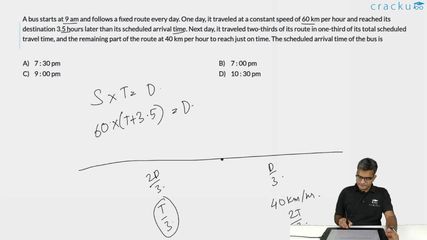
A bus starts at 9 am and follows a fixed route every day. One day, it traveled at a constant speed of 60 km per hour and reached its destination 3.5 hours later than its scheduled arrival time. Next day, it traveled two-thirds of its route in one-third of its total scheduled travel time, and the remaining part of the route at 40 km per hour to reach just on time. The scheduled arrival time of the bus is

Let's take the scheduled time taken by the bus to be t
From the first statement (bus travelling at 60 kmph), we can get the total distance travelled by bus to 60(t+3.5)

The second scenario gives us that the bus covered two-thirds of the distance in one-third of the time, meaning that the remaining one-third distance was covered in two-thirds of the time, giving us the relation $$\frac{1}{3}st$$ covered in $$\frac{2}{3}t$$ giving the speed to be $$\frac{s}{2}$$ which is given as 40 km/h, thereby giving the usual speed of the bus to be 80 km/hr

Now the first relation we get 60(t+3.5)=80t
Giving us t=10.5 hours

Thus, the bus usually takes 10.5 hours on its journey. 
Staring at 9:00, it will complete the journey at 7:30 pm

Therefore, Option A is the correct answer.