Question 100

Let T be the triangle formed by the straight line 3x + 5y - 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is

Name: Let T be the triangle formed by the straight line 3x + 5y - 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is
Uploaded: May 3, 2022, 4:55 p.m.
Duration: 2 min 49 s
Description: Let T be the triangle formed by the straight line 3x + 5y - 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is

Correct Answer: 9

Solution

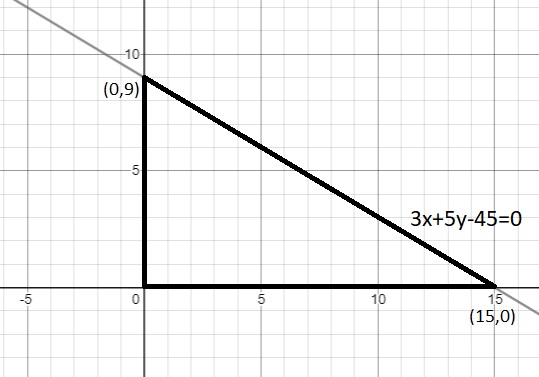
In any right triangle, the circumradius is half of the hypotenuse. Here,L=$$\ \frac{\ 1}{2}\ $$* the length of the hypotenuse = $$\ \frac{\ 1}{2}$$($$\sqrt{\ 15^2+9^2}$$) = $$\ \frac{\ 1}{2}\ $$*$$\sqrt{\ 306}$$ = $$\ \frac{\ 1}{\ 2}\times\ $$17.49 = 8.74

Hence, the integer close to L = 9

Share on Whatsapp Share on Whatsapp

Boost your CAT prep: Take All-India 3 free CAT mock tests with Video solutions

Video Solution

Click on the Email ☝️ to Watch the Video Solution

Create a FREE account and get:

All Quant CAT complete Formulas and shortcuts PDF
35+ CAT previous year papers with video solutions PDF
5000+ Topic-wise Previous year CAT Solved Questions for Free

CAT Quant Questions | CAT Quantitative Ability

CAT Logarithms Questions CAT Logarithms, Surds and Indices Questions CAT Averages, Ratio and Proportion Questions CAT Functions, Graphs and Statistics Questions CAT Probability, Combinatorics Questions

CAT DILR Questions | LRDI Questions For CAT

CAT Data change over a period Questions CAT Special Charts Questions CAT DI with connected data sets Questions CAT Quant Based DI Questions CAT Scheduling Questions

CAT Verbal Ability Questions | VARC Questions For CAT

CAT Verbal Ability Questions CAT Critical Reasoning Questions CAT Miscellaneous Questions CAT Reading Comprehension Questions CAT Para Jumbles Questions

Also Read

CAT Mock Tests

CAT 2025 Course

Free CAT Preparation

CAT Questions

CAT Formulas PDF

CAT Study Material

CAT Score vs Percentile

CAT Percentile Predictor

CAT Sectional Tests

CAT Exam

CAT Prep Videos

CAT Registration

CAT Syllabus 2025

CAT Eligibility Criteria

CAT Admit Card

CAT Score Calculator

CAT 2019 QA Slot 1 Question

Let T be the triangle formed by the straight line 3x + 5y - 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is

Video Solution

CAT Quant Questions | CAT Quantitative Ability

CAT DILR Questions | LRDI Questions For CAT

CAT Verbal Ability Questions | VARC Questions For CAT

Also Read

Free CAT Quant Questions

Login to your Cracku account

Hello! 👋

Ready to Unlock Your Success?

Please Enter Your OTP

Please enter the following details

Create a free Cracku account

Get Started with 5000+ Free CAT Questions & Mock Tests with Detailed Solutions!