A girl travels along a straight line, from point A to B at a constant speed, $$V_1$$ meters/sec for T seconds. Next, she travels from point B to C along a straight line, at a constant speed of $$V_2$$ meters/sec for another T seconds. BC makes an angle 105° with AB. If CA makes an angle 30° with BC, how much time will she take to travel back from point C to A at a constant speed of $$V_2$$ meters/sec, if she travels along a straight line from C to A?
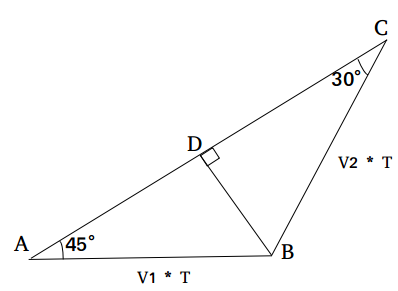
We draw BD perpendiculat to AC.
In right angled triangle BDC, BD / BC = sin 30°
or, BD = (V2 * T)/2 ......(i)
In right angled triangle BDA, BD / BA = sin 45°
Or, BD = (V1 * T)/$$\sqrt{2}$$ ......(ii)
From (i) and (ii), we get
V2 / V1 = $$\sqrt{2}$$
Total distance to be travelled from C to A = CD + DA = $$\sqrt{3}$$BD + BD
= BD($$1 + \sqrt{3}$$)
Replacing BD = (V2 * T)/2 in the avove equation,
CA = $$\dfrac{\text{(V2 * T)}}{2} (1 + \sqrt{3}$$)
Time taken at speed V2 = $$0.5(\sqrt{3}+1)$$T
Hence, option C is the correct answer.




