How many ATMs have cash requirements of Rs. 10 Lakhs or more?

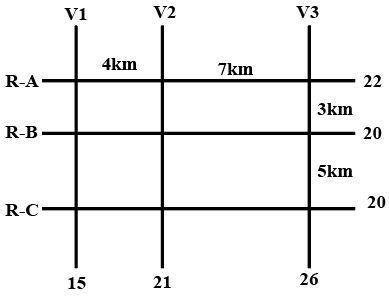
This is the figure that has been given to us,

We are given the information that, out of the 9 intersections in the figure, 6 of them have ATMs. That means, 3 of these intersections are empty.
We are also told that, the ATMs with the highest and lowest capacity are on the same road, highest capacity being 15L and lowest being 7L.
This information not only gives us clues about the location of these two ATMs but also, now we know the upper and lower bounds for cash in the six ATMs with distinct cash.
Next piece of information that is given is that, road distance between the ATM with the second highest cashrequirement and the ATM located at the intersection of R-C and V3 is12 km. Since we can only traverse on the roads, from (RC, V3) we have to either traverse the 5km road or the 7km road. The only way it can add up to 12 is 5+7. That means, ATM with the second highest capacity is at (RB, V2).

Now, let us start arranging the ATM's.
We are told that 15 and 7 are on the same road. Since we are given the total capacities on the roads, we need to identify the roads with capacity higher or equal to 22.
There are only two possible choice, either RA or V3.
Looking at V3, we see that 15L ATM cannot come at (RB, V3) or (RC, V3) since the RB and RC capacity is 20, and the minimum ATM limit is 7L, if a 15L ATM is on a road with total capacity 20L, this is a situation that is not possible since there cannot be an ATM with 5L capacity.
The same is the case with the intersection (RA, V2). So, we can narrow down the fact that the 15L ATM has to either be at (RA, V1) or (RA, V3)

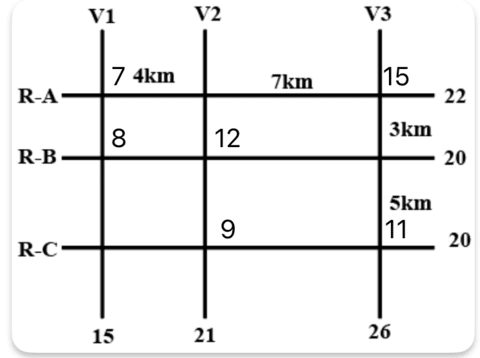
Case 1: 15L ATM is on the intersection (RA, V3)

We see that, for V3 to add upto 26, there has to be an ATM with cash of 11L, there cannot be two ATM's since the minimum capacity is 7L.
We can place the 11L ATM at (RB, V3) or (RC, V3), if we place them at either of these intersections, the remaining ATM has to have a capacity of 9L for the same reason. 9L cannot be at (RC, V1) or (RB, V1) since the total capacity of V1 is 15L and there cannot be an ATM with 6L. And it also cannot be at (RB, V2) since there is already an ATM with 11L that means the ATM with the second highest capacity cannot be 9. So that means 9L has to be at (RC, V2). And then filling in the rest of the numbers we get the final arrangement for Case-1.

Case 2: When 15L is at (RA, V1)
There can be no other ATM on V1 in this scenario, 7L ATM which is on RA cannot be on (RA, V2) considering the sum of the numbers on V2 is 21, and there cannot be 7+7 or a 14L ATM since the capacity of both RB and RC is 20. So, 7L has to be on V3, and since there cannot be a single ATM of 19L on V3, there has to be two other ATMs on V3 adding up to 19. Rearranging the numbers, we get the scenario for the second case.

Using the two cases, we can answer the given questions.

Three ATM's with 10L or more: 15L, 12L and 11L. Answer is 3.