Please enter the following details
Free Daily Targets & Mocks
Study Material & Formulas PDFs
1 on 1 Mentorship
Question 3
$$\triangle$$ABC and $$\triangle$$XYZ are equilateral triangles of 54 cm sides. All smaller triangles like $$\triangle$$ANM, $$\triangle$$OCP, $$\triangle$$QPX etc. are also equilateral triangles. Find the area of the shape MNOPQRM.
Solution
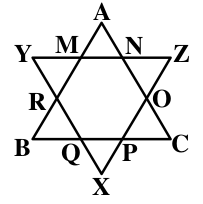
AB = 54 cm and $$\triangle$$ANM , $$\triangle$$OCP , $$\triangle$$OPX are equilateral triangles.
=> MN = MR = NO = OP = PQ = QR = $$\frac{54}{3} = 18$$ cm
Thus,  MNOPQRM is a regular hexagon with side 18 cm
$$\therefore$$ Area of  MNOPQRM = $$\frac{3 \sqrt{3}}{2} (side)^2$$
= $$\frac{3 \sqrt{3}}{2} \times 18^2 = 486 \sqrt{3} cm^2$$
XAT Quant Questions | XAT Quantitative Ability
XAT Linear Equations QuestionsXAT Venn Diagrams QuestionsXAT Functions, Graphs and Statistics QuestionsXAT Profit, Loss and Interest QuestionsXAT Number Systems Questions
XAT DILR Questions | LRDI Questions For XAT
XAT Special Charts QuestionsXAT DI with connected data sets QuestionsXAT Data Interpretation QuestionsXAT Scheduling QuestionsXAT Selection With Condition Questions
