Funky Pizzeria was required to supply pizzas to three different parties. The total number of pizzas it had to deliver was 800, 70% of which were to be delivered to Party 3 and the rest equally divided between Party 1 and Party 2.
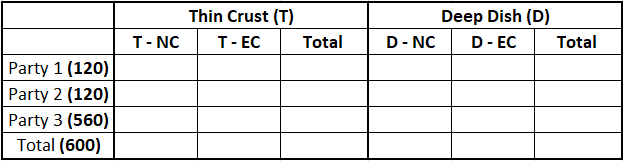
Pizzas could be of Thin Crust (T) or Deep Dish (D) variety and come in either Normal Cheese (NC) or Extra Cheese (EC) versions. Hence, there are four types of pizzas: T-NC, T-EC, D-NC and D-EC. Partial information about proportions of T and NC pizzas ordered by the three parties is given below:

For Party 2, if 50% of the Normal Cheese pizzas were of Thin Crust variety, what was the difference between the numbers of T-EC and D-EC pizzas to be delivered to Party 2?
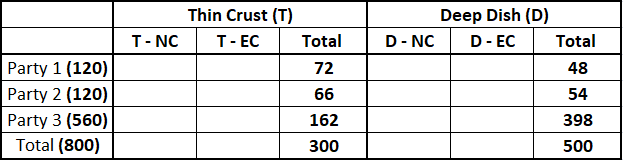
We are given that Party 3 received 70% of total pizzas,therefore, number of pizzas received by Party 3 = $$\frac{70}{100}\times 800$$ = 560
Remaining 240 pizzas are equally divided among party 1 and party 2 hence we can say that each of Party 1 and Party 2 received 120 pizzas.
We know that all of the pizza can be classified into a total of 4 types. Hence, on drawing a table which can accommodate all of the cases:
Total number of Thin Crust pizzas = 0.375*800 = 300. Therefore, total number of Deep Dish pizzas = 800 - 300 = 500.
Out of 120 pizzas that Party 1 received, 60% were of Thin Crust type hence, total number of Thin Crust pizza received by Party 1 = 0.6*120 = 72. Consequently Party 1, must have received 42 Deep Dish type pizzas.
Out of 120 pizzas that Party 2 received, 55% were of Thin Crust type hence, total number of Thin Crust pizza received by Party 2 = 0.55*120 = 66. Consequently Party 1, must have received 54 Deep Dish type pizzas.
Therefore, total number of Thin Crust pizzas ordered by Party 3 = Total Thin Crust pizzas ordered - Thin Crust pizzas ordered by Party 1 - Thin Crust pizzas ordered by Party 2
$$\Rightarrow$$ 300 - 72 - 66 = 162
Hence number of Deep Dish type of pizzas order by Party 3 = 560 - 162 = 398
Number of Normal Cheese pizzas require to be delivered to Party 2 = 0.3*120 = 36
It is given that 50% of these Normal Cheese pizzas were of Thin Crust variety, then We can say that remaining 50% were of Deep Dish variety. We can find out each of 4 types of pizzas require to be delivered to Party 2.
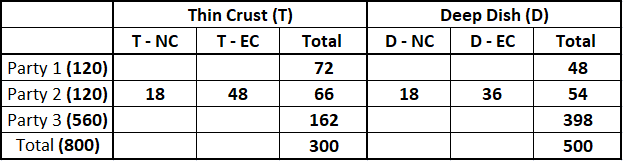
Hence, the difference between the numbers of T-EC and D-EC pizzas to be delivered to Party 2 = 48 - 36 = 12
Therefore, option B is the correct answer.
Video Solution

Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free




