In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. If both the chords are on the same side of the centre, then the distance between the chord is
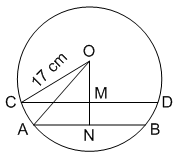
Given : CD = 30 cm and AB = 16 cm
To find : MN = ?
Solution : Perpendicular distance from the centre bisects the chord.
=> CM = $$\frac{30}{2}=15$$ cm and AN = $$8$$ cm
Now, in $$\triangle$$ OCM,
=> $$(OM)^2=(OC)^2-(CM)^2$$
=> $$(OM)^2=(17)^2-(15)^2$$
=> $$(OM)^2=289-225=64$$
=> $$OM=\sqrt{64}=8$$ cm
Similarly, in $$\triangle$$ OAN,
=> $$(ON)^2=(OA)^2-(AN)^2$$
=> $$(ON)^2=(17)^2-(8)^2$$
=> $$(ON)^2=289-64=225$$
=> $$ON=\sqrt{225}=15$$ cm
$$\therefore$$ MN = ON - OM
= $$15-8=7$$ cm
=> Ans - (B)
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free

