AB is the chord of a circle with centre O and DOC is a line segement originating from a point D on the circle and intersecting AB produced at C such that BC = OD. If $$\angle$$BCD =$$20^{\circ}$$, then $$\angle$$AOD =?
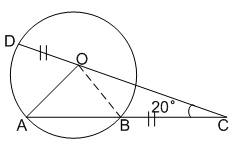
It is given that OD = BC and OD = OB (radii of circle)
=> OB = BC
=> $$\angle$$ BCO = $$\angle$$ BOC = $$20^\circ$$ (Angle opposite to equal sides are equal)
Then, $$\angle$$ OBC = $$180^\circ-(\angle BCO +\angle BOC)$$
=> $$\angle$$ OBC = $$180^\circ-20^\circ-20^\circ=140^\circ$$
Also, $$\angle$$ OBA + $$\angle$$ OBC = $$180^\circ$$ (Linear pair)
=> $$\angle$$ OBA = $$\angle$$ OAB = $$180^\circ-140^\circ=40^\circ$$
Now, $$\angle$$ AOB = $$180^\circ-(\angle OAB +\angle OBA)$$
=> $$\angle$$ AOB = $$180^\circ-40^\circ-40^\circ=100^\circ$$
$$\therefore$$ $$\angle$$ AOD = $$180^\circ-(\angle AOB +\angle BOC)$$ (Linear pair)
= $$180^\circ-100^\circ-20^\circ=60^\circ$$
=> Ans - (D)
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free

