If the diagonals of a rhombus of side 15 cm are in the ratio 3:4, find the area of the rhombus.

It is given that the length of the diagonals are in 3:4. Let '3x', and '4x' be the lengths of semi-diagonals as shown in the figure. We know that diagonals of a rhombus intersect each other perpendicularly.

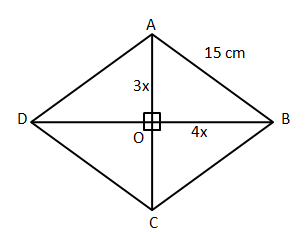
In right angle triangle AOB,
$$AB^2=AO^2+BO^2$$

$$\Rightarrow$$ $$AB= \sqrt{AO^2+BO^2}$$

$$\Rightarrow$$ $$AB= \sqrt{(3x)^2+(4x)^2}$$

$$\Rightarrow$$ $$15= 5x$$

$$\Rightarrow$$ $$x= 3$$cm.

Therefore, we can say that the length of diagonals = 6x and 8x or 18 and 24 cm.

Hence, the area of the rhombus = $$\dfrac{1}{2}*18*24$$ = 216 cm$$^2$$. Therefore, option E is the correct answer.