A tall tower has its base at point K. Three points A, B and C are located at distances of 4 metres, 8 metres and 16 metres respectively from K. The angles of elevation of the top of the tower from A and C are complementary.

What is the angle of elevation (in degrees) of the tower’s top from B?

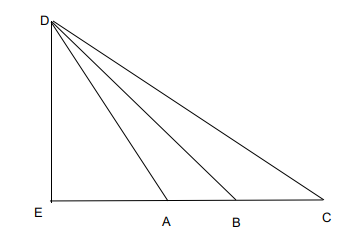
Given the distances are :

AE = 4 meters , EB = 8 meters and EC = 16 meters.

Considering the length of ED = K.

Given the angles DAE and angle DCE  are complementary.

Hence the angles are A and 90 - A.

Tan(90-A) = Cot A

$$\ \tan\ DAE\ =\frac{k}{4}$$ and $$\ \tan\ DCE\ =\frac{1}{\tan\ DAE}=\ \frac{k}{16}$$

Hence $$\frac{k}{16}=\ \frac{4}{k}$$

k = 8 meters.

The angle DBE is given by 

$$Tan\ DBE\ =\ \frac{k}{8}=\ 1$$

Hence the angle is equal to 45 degrees.