Let C be a circle of radius $$\sqrt{20}$$ cm. Let L1, L2 be the lines given by 2x − y −1 = 0 and x + 2y−18 = 0, respectively. Suppose that L1 passes through the center of C and that L2 is tangent to C at the point of intersection of L1 and L2. If (a,b) is the center of C, which of the following is a possible value of a + b?
As mentioned in the question,
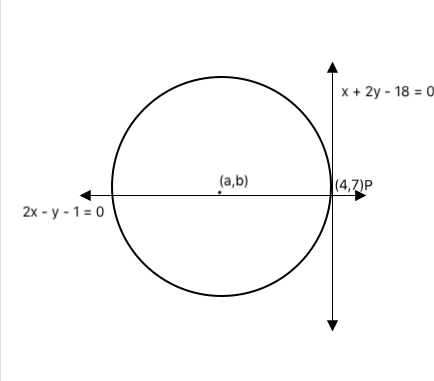
Lines L1 and L2 intersect at point P as shown in the figure.
On solving for x and y from equations
x + 2y - 18 = 0
2x - y - 1 = 0
We get x = 4 and y =7.
Given, radius = $$\sqrt{20}$$
Using the equation of a circle, we have
$$(4-a)^{2}$$ + $$(7-b)^{2}$$ = 20....(1)
The center of the circle will lie on the line: 2x - y - 1 = 0
a,b will satisfy this equation.
So 2a-b-1=0
b=2a-1
From equation 1...
$$(4-a)^{2}$$ + $$(7-b)^{2}$$ = 20
$$(4-a)^{2}$$ + $$(8-2a)^{2}$$ = 20
5$$(4-a)^{2}$$ = 20
a=6 or a=2
b=11 or b=3
The sum of the coordinates possible=6+11 or 2+3
i.e. 17 or 5
Option B is one of the solution.
Video Solution

Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE




