Please enter the following details
Free Daily Targets & Mocks
Study Material & Formulas PDFs
1 on 1 Mentorship
Question 59
A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is
Solution
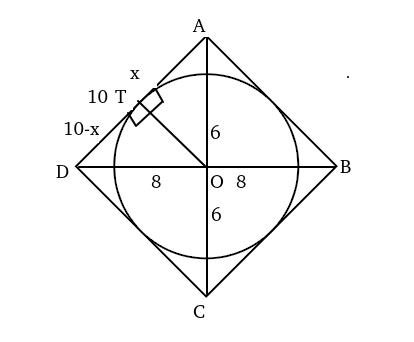
Let the length of radius be 'r'.
From the above diagram,
$$x^2+r^2=6^2\ $$....(i)
$$\left(10-x\right)^2+r^2=8^2\ $$----(ii)
Subtracting (i) from (ii), we get:
x=3.6 => $$r^2=36-\left(3.6\right)^2$$ ==> $$r^2=36-\left(3.6\right)^2\ =23.04$$.
Area of circle = $$\pi\ r^2=23.04\pi\ $$
Area of rhombus= 1/2*d1*d2=1/2*12*16=96.
.'. Ratio of areas = 23.04$$\pi\ $$/96=$$\frac{6\pi}{25}$$
Video Solution
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
CAT Quant Questions | CAT Quantitative Ability
CAT Profit, Loss and Interest QuestionsCAT Remainders QuestionsCAT Geometry QuestionsCAT Averages Mixtures Alligations QuestionsCAT Averages Questions
CAT DILR Questions | LRDI Questions For CAT
CAT Data Interpretation QuestionsCAT Selection With Condition QuestionsCAT Charts QuestionsCAT DI Miscellaneous QuestionsCAT Special Charts Questions
