The area of a right angled triangle ABC, right angled at B, is 46 sq units. A median is drawn from A to BC which intersects at D. Find the area (in sq. units) of triangle ABD.

Note :- A median divides a triangle into two parts of equal areas.

Proof :

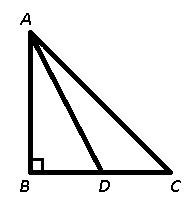
It is given that $$ar(\triangle ABC)=46$$ sq.units

Also, AD bisects BC, let BC = $$2x$$ units => BD = $$\frac{2x}{2}=x$$ units

$$\therefore$$ $$\frac{ar(\triangle ABD)}{ar(\triangle ABC)}=\frac{\frac{1}{2}\times(AB)\times(BD)}{\frac{1}{2}\times(AB)\times(BC)}$$

=> $$\frac{\triangle}{46}=\frac{x}{2x}$$

=> $$\triangle=\frac{46}{2}=23$$ sq.units

=> Ans - (B)