In a triangle ABC, a line is drawn from C which bisects AB at point D. Find the ratio of area of the triangles DBC and ABC.
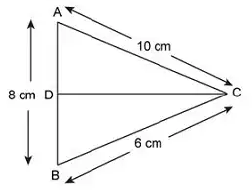

Given : CD bisects AB, => AD = DB = $$\frac{8}{2}=4$$ cm
To find : $$\frac{ar(\triangle DBC)}{ar(\triangle ABC)}=?$$
Solution : Clearly $$\triangle$$ ABC is a right angled triangle, $$\because (10)^2=(8)^2+(6)^2$$
Thus, AC is the hypotenuse and $$\triangle$$ ABC is right angled at B.
=> AB = 8 cm is the height of triangle
$$\therefore$$ $$\frac{ar(\triangle DBC)}{ar(\triangle ABC)}=\frac{\frac{1}{2}\times(DB)\times(BC)}{\frac{1}{2}\times(AB)\times(BC)}$$
= $$\frac{4\times6}{8\times6}=\frac{1}{2}$$
=> Ans - (C)
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free
