XAT 2014 Question Paper - QUANT
For the following questions answer them individually
$$x, 17, 3x - y^{2} - 2$$, and $$3x + y^{2} - 30$$, are four consecutive terms of an increasing arithmetic sequence. The sum of the four number is divisible by:
In quadrilateral PQRS, PQ = 5 units, QR = 17 units, RS = 5 units, and PS = 9 units. The length of the diagonal QS can be:
There are two windows on the wall of a building that need repairs. A ladder 30 m long is placed
against a wall such that it just reaches the first window which is 26 m high. The foot of the
ladder is at point A. After the first window is fixed, the foot of the ladder is pushed backwards
to point B so that the ladder can reach the second window. The angle made by the ladder with the
ground is reduced by half, as a result of pushing the ladder. The distance between points A and B is
Amitabh picks a random integer between 1 and 999, doubles it and gives the result to Sashi. Each
time Sashi gets a number from Amitabh, he adds 50 to the number, and gives the result back to Amitabh, who doubles the number again. The first person, whose result is more than 1000, loses the game. Let ‘x’ be the smallest initial number that results in a win for Amitabh. The sum of the digits of ‘x’ is:
Consider four natural numbers: x, y, x + y, and x - y. Two statements are provided below:
I. All four numbers are prime numbers.
II. The arithmetic mean of the numbers is greater than 4.
Which of the following statements would be sufficient to determine the sum of the four numbers?
Triangle ABC is a right angled triangle. D and E are mid points of AB and BC respectively. Read
the following statements.
I. AE = 19
II. CD = 22
III. Angle B is a right angle.
Which of the following statements would be sufficient to determine the length of AC?
There are two circles $$C_{1}$$ and $$C_{2}$$ of radii 3 and 8 units respectively. The common internal tangent, T, touches the circles at points $$P_{1}$$ and $$P_{2}$$ respectively. The line joining the centers of the circles intersects T at X. The distance of X from the center of the smaller circle is 5 units. What is the length of the line segment $$P_{1} P_{2}$$ ?
Consider the formula, $$S=\frac{\alpha\times\omega}{\tau+\rho\times\omega}$$ positive integers. If ⍵ is increased and ⍺, τ and ρ are kept constant, then S:
Prof. Suman takes a number of quizzes for a course. All the quizzes are out of 100. A student can get an A grade in the course if the average of her scores is more than or equal to 90.Grade B is awarded to a student if the average of her scores is between 87 and 89 (both included). If the average is below 87, the student gets a C grade. Ramesh is preparing for the last quiz and he realizes that he will score a minimum of 97 to get an A grade. After the quiz, he realizes that he will score 70, and he will just manage a B. How many quizzes did Prof. Suman take?
A polynomial y=$$ax^{3} + bx^{2 }+ cx + d$$ intersects x-axis at 1 and -1, and y-axis at 2. The value of b is:
The probability that a randomly chosen positive divisor of $$10^{29}$$ is an integer multiple of $$10^{23}$$ is: $$a^{2} /b^{2} $$, then ‘b - a’ would be:
Circle $$C_{1}$$ has a radius of 3 units. The line segment PQ is the only diameter of the circle which is parallel to the X axis. P and Q are points on curves given by the equations $$y = a^{x} and y = 2a^{x}$$ respectively, where a < 1. The value of a is:
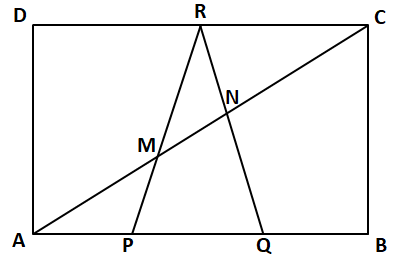
Consider a rectangle ABCD of area 90 units. The points P and Q trisect AB, and R bisects CD. The
diagonal AC intersects the line segments PR and QR at M and N respectively. What is the area of the quadrilateral PQNM?
Two numbers, $$297_{B}$$ and $$792_{B}$$ , belong to base B number system. If the first number is a factor of the second number then the value of B is:
A teacher noticed a strange distribution of marks in the exam. There were only three distinct
scores: 6, 8 and 20. The mode of the distribution was 8. The sum of the scores of all the students was 504. The number of students in the in most populated category was equal to the sum of the number of students with lowest score and twice the number of students with the highest score. The total number of students in the class was:
Read the following instruction carefully and answer the question that follows:
Expression $$\sum_{n=1}^{13}\frac{1}{n}$$ can also be written as $$\frac{x}{13!}$$ What would be the remainder if x is divided by 11?
A rectangular swimming pool is 48 m long and 20 m wide. The shallow edge of the pool is 1 m deep.
For every 2.6 m that one walks up the inclined base of the swimming pool, one gains an elevation of 1 m. What is the volume of water (in cubic meters), in the swimming pool? Assume that the pool is filled up to the brim.v
There are two squares S 1 and S 2 with areas 8 and 9 units, respectively. S 1 is inscribed within S 2 , with one corner of S 1 on each side of S 2 . The corners of the smaller square divides the sides of
the bigger square into two segments, one of length ‘a’ and the other of length ‘b’, where, b > a. A possible value of ‘b/a’, is:
Diameter of the base of a water - filled inverted right circular cone is 26 cm. A cylindrical pipe, 5 mm in radius, is attached to the surface of the cone at a point. The perpendicular distance
between the point and the base (the top) is 15 cm. The distance from the edge of the base to the
point is 17 cm, along the surface. If water flows at the rate of 10 meters per minute through the
pipe, how much time would elapse before water stops coming out of the pipe?
Aditya has a total of 18 red and blue marbles in two bags (each bag has marbles of both colors). A
marble is randomly drawn from the first bag followed by another randomly drawn from the
second bag, the probability of both being red is 5/16. What is the probability of both marbles being blue?
Answer the questions based on the given data on the tourism sector in India.

In which of the following years the percentage increase in the number of Indians going abroad was greater than the percentage increase in the number of domestic tourists?
Let ‘R’ be the ratio of Foreign Exchange Earnings from Tourism in India (in US $ million) to Foreign Tourist Arrivals in India (in million). Assume that R increases linearly over the years. If we draw a pie chart of R for all the years, the angle subtended by the biggest sector in the pie chart would be approximately:
Answer the questions based on the following information given below.
The exhibit given below compares the countries (first column) on different economic indicators (first row), from 2000-2010. A bar represents data for one year and a missing bar indicates missing data. Within an indicator, all countries have same scale.
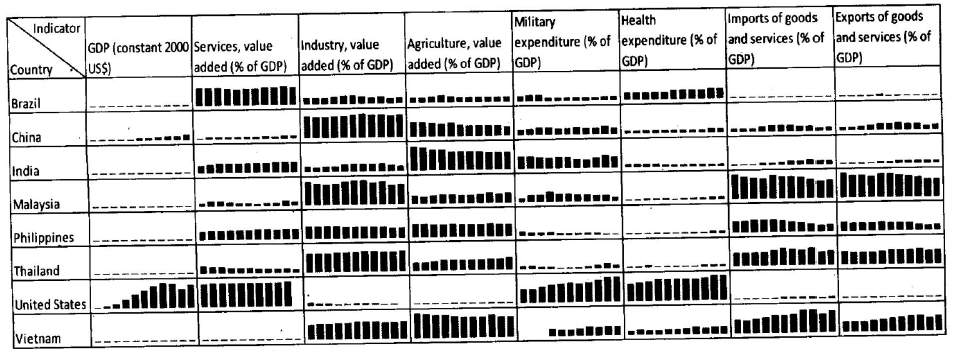
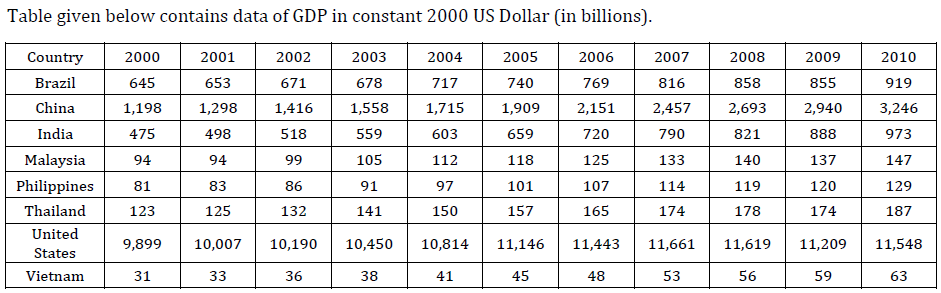
Which of the following countries, after United States, has the highest spending on military as % of GDP, in the period 2000-2010?
Which country (and which year) has witnessed maximum year-to-year decline in “industry as percentage of GDP”? Given that the maximum value of industry as percentage of GDP is 49.7% and the minimum value of industry as percentage of GDP is 20.02%, in the chart above.
Which of the following countries has shown maximum increase in the “services, value added as % of GDP” from year 2000 to year 2010?
Answer the questions based on the trends lines from the following graphs.
Note: Left side of X axis represents countries that are “poor” and right side of X axis represents countries that are “rich”, for each region. GDP is based on purchasing power parity (PPP).
These are World Bank (WB) estimates.

Which of the following could be the correct ascending order of democratic regions for poor?
Which region has the highest disparity, of democratic participation, between rich and poor?
The maximum GDP of African region is higher than the maximum GDP of South American region by factor of:
Two Factor Authentication
Incase of any issue contact support@cracku.in