Question 2
ABC is a triangle. The bisectors of the internal angle $$\angle$$B and external $$\angle$$C intersect at D. If $$\angle$$BDC=$$50^{\circ}$$, then $$\angle$$A is
Solution
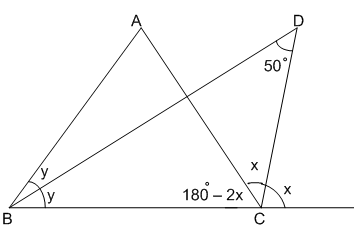
In $$\triangle$$ BDC,
=> $$y+(180^\circ-2x+x)+50^\circ=180^\circ$$
=> $$y-x+50^\circ=0$$
=> $$y-x=-50^\circ$$
In $$\triangle$$ ABC,
=> $$2y+(180^\circ-2x)+\angle A=180^\circ$$
=> $$2(y-x)+\angle A=0$$
=> $$2(-50^\circ)+\angle A=0$$
=> $$\angle A=100^\circ$$
=> Ans - (A)
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free
