Determine the value(s) of “a” for which the point $$(a, a^{2})$$ lies inside the triangle formed by the lines: 2x+ 3y= 1, x+ 2y=3 and 5x-6y= 1
Let us draw the diagram first,
Let L$$_{1}$$: 2x+ 3y -1 = 0
L$$_{2}$$: x+ 2y -3 = 0
L$$_{3}$$: 5x-6y- 1 = 0
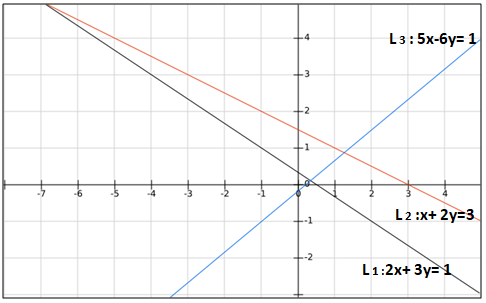
With respect to L$$_{1}$$, we can see that the point $$(a, a^{2})$$ lies within the triangle and (0, 0) are opposite side. Therefore,
L$$_{(a, a^2)}$$* L$$_{(0, 0)}$$ < 0
$$\Rightarrow$$ $$(2a+ 3a^2-1)(-1)<0$$
$$\Rightarrow$$ $$(3a^2+2a-1)>0$$
$$\Rightarrow$$ a < -1 or a > $$\frac{1}{3}$$ ... (1)
With respect to L$$_{2}$$, we can see that the point $$(a, a^{2})$$ lies within the triangle and (0, 0) are on the same side. Therefore,
L$$_{(a, a^2)}$$* L$$_{(0, 0)}$$ > 0
$$\Rightarrow$$ $$(a+ 2a^2-3)(-3)>0$$
$$\Rightarrow$$ $$(2a^2+a-3)<0$$
$$\Rightarrow$$ $$\frac{-3}{2}$$ < a < 1 ... (2)
With respect to L$$_{3}$$, we can see that the point $$(a, a^{2})$$ lies within the triangle and (0, 0) are on the same side. Therefore,
L$$_{(a, a^2)}$$* L$$_{(0, 0)}$$ > 0
$$\Rightarrow$$ $$(5a- 6a^2-1)(-1)>0$$
$$\Rightarrow$$ $$(6a^2-5a+1)>0$$
$$\Rightarrow$$ a < $$\frac{1}{3}$$ or a > $$\frac{1}{2}$$ ... (3)
From equation (1), (2) and (3) we can say that
a $$\epsilon$$ (-3/2,-1) ⋃ (1/2, 1). Hence, option C is the correct answer.
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE




