Read the following case  – let and answer the that follow

Ms. Banerjee, class teacher for 12th standard, wants to send teams (based on past performance) of three students each to district, state, national, and international competition in mathematics.Till now, every student of the class has appeared in 100 school level tests. The students had following distribution of marks in the tests, in terms of “average” and “number of times a student scored cent per cent marks”.

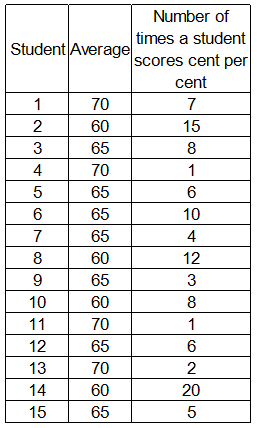
Ms. Banerjee has carefully studied chances of her school winning each of the competitions. Based on in - depth calculations, she realized that her school is quite likely to win district level competition but has low chances of winning the international competition. She listed down the following probabilities of wins for different competitions. Prize was highest for international competition and lowest for district level competition (in that order).

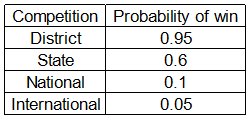
All the students are studying in the school for last twelve years. She wanted to select the best team for all four competitions (Ms. Banerjee had no other information to select students).