Read the following case – let and answer the that follow
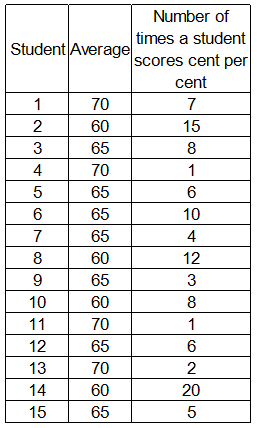
Ms. Banerjee, class teacher for 12th standard, wants to send teams (based on past performance) of three students each to district, state, national, and international competition in mathematics.Till now, every student of the class has appeared in 100 school level tests. The students had following distribution of marks in the tests, in terms of “average” and “number of times a student scored cent per cent marks”.
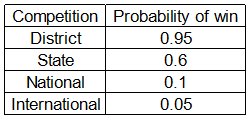
Ms. Banerjee has carefully studied chances of her school winning each of the competitions. Based on in - depth calculations, she realized that her school is quite likely to win district level competition but has low chances of winning the international competition. She listed down the following probabilities of wins for different competitions. Prize was highest for international competition and lowest for district level competition (in that order).
All the students are studying in the school for last twelve years. She wanted to select the best team for all four competitions (Ms. Banerjee had no other information to select students).
Ms. Banerjee has to select the team for national competition after she has selected the team for
international competition. A student selected for international competition cannot be a part of national competition. Which is the best team for the national competition?
Ms Banarjee selects the national team only after selecting the international team :
For selection of international team our choices must be focused on people with high number of cent percents because the probability of success is low need some one securing high cent percent and low averages so that we do not waste people with higher averages in a case where the chances of success are very low .
Hence we select 2, 8, 14 who are having an average of 60 which is the lowest and high cent percents which are 12 +15+20 =47.
Since 2,8,14 are selected they cannot be used while selecting the national team.Now while selecting the national team the probability is success is relatively low but still improved from the international competition and since 2,8,14 are already selected we cannot use them and coming to the first option 1,4,7 has people with very high averages and lower cent percentage and hence does not fit our criteria.
The best option is option D where people are averaged in relatively better and also holds good number of cent percents.
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE




