A container is filled with liquid, 6 part of which are water and 10 part milk. How much of the mixture must be drawn off and replaced with water, so that the mixture may be half water and half milk?
Given that currently container has 6 parts of water and 10 parts of milk.
Assume the volume of water to be $$6x$$ and that of milk to be $$10x$$
So, the volume of the container is $$16x$$.
Assume we take out $$y$$ litre of mixture and replace it with water
So, the resultant mixture will have
$$\left(6x-\dfrac{6x}{16x}\times y+y\right)$$ water and
$$\left(10x-\dfrac{10x}{16x}\times y\right)$$ milk
Given the volume of water is half of the container i.e. $$8x$$
So, $$\left(10x-\dfrac{10x}{16x}\times y\right)=8x$$
$$10x-\dfrac{5}{8}y=8x$$
or, $$y=\dfrac{16x}{5}$$
In terms of container volume
$$\dfrac{y}{16x}=\dfrac{\dfrac{16x}{5}}{16x}=\dfrac{1}{5}$$
Hence, the answer is Option C
Video Solution
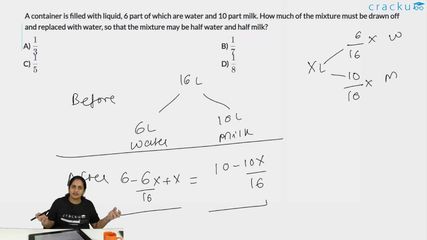
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 40+ previous papers with detau solutions PDF
- Top 500 MBA exam Solved Questions for Free




