Read the following scenario and answer the THREE questions that follow.
A pencil maker ships pencils in boxes of size 50, 100 and 200. Due to packaging issues, some pencils break. About the 20 boxes he has supplied to a shop, the following information is available:
* Box no. 1 through 6 have 50 pencils, Box no. 7 through 16 have 100 pencils and Box no. 17 through 20 have 200 pencils.
* No box has less than 5% or more than 20% broken pencils.
Following is the frequency table of the number of broken pencils for the twenty boxes:
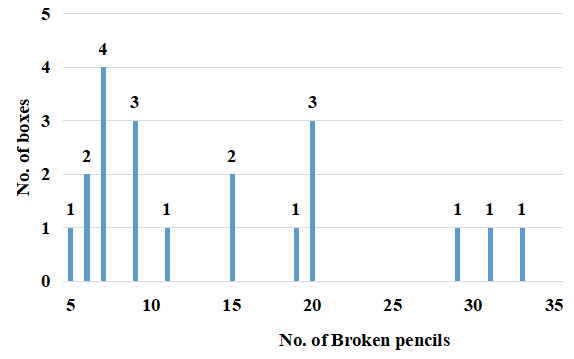
Which of the following can possibly be the sequence of the number of brokenpencils in Boxes 7-16?
Boxes 7 to 16 contain a total of 100 pencils each. The minimum number of broken pencils the box can hold is 5 percent of the total pencils and a maximum of 20 percent of the total pencils.
5 percent of 100 = 5 and 20 percent of 100 = 20 pencils.
Hence the number of broken pencils must be in the range of 5 to 20.
The frequency of the different number of broken pencils is :
5 - 1
6 - 2
7 - 4
9 - 3
11 - 1
15 - 2
19 - 1
20 - 3
29 - 1
31 - 1
33 - 1
The boxes cannot contain 29, 31, 33 to be the number of broken pencils because they are beyond 20 percent.
Since boxes 1- 6 can contain only between 2.5 to 10 pencils. The remaining boxes which include broken pencils of numbers less than 10 must be a part of 7 - 16. Because boxes 17 - 20 cannot contain broken pencils of numbers less than 10.
Hence 7 - 16 must have 4 boxes that contain less than 10 broken pencils.
Going through the options :
Option A fails because this includes only 3 boxes with less than 10 pencils.
Option B fails because we only have 2 boxes with 6 broken pencils but this includes 3.
Option D fails because it does not include a box of 15 and a box of 20 pencils which can only be a part of boxes with 100 or boxes with 200 pencils. Since boxes 17 - 20 can include only one among 15 or 20 because 29, 31, 33 are a part of this group. Hence this case fails.
Option E fails because this includes 5 boxes with broken pencils less than 10 but this is not possible because this must exactly contain 4 boxes with less than 10 pencils.
Option C is a feasible case containing :
1-6 ( 5, 6, 6, 9, 9, 9)
7 - 16 ( 7, 7, 7, 7, 11, 15, 15, 19, 20, 20 )
17 - 20 (20, 29, 31, 33)
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE




