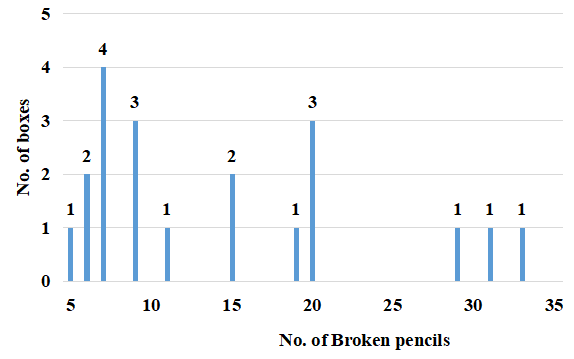
Suppose that additionally it is known that the number of broken pencils in Boxes 17-20 are in increasing order. Which among the following additional information, if true, is not sufficient to uniquely know the number of defective pencils in each of the boxes numbered 17-20?

Going by the options :

Option A: Boxes 7- 16 contain a total of 124 pencils. Boxes (1-6) has 6 boxes with broken pencils which can be included from :

(5, 6, 6, 7, 7, 7, 7, 9, 9, 9). The minimum possible sum of the 6 pencils is : (5+6+6+7) = 24 and the maximum possible sum is (7+9+9+9) = 34.

Boxes 7 - 16 contains all the boxes with broken pencils except one among the boxes with broken pencils among 11 - 20 and hence ;

This can contain : (11+15+15+19+20+20) or (15+15+19+20+20+20)  or (11+15+15+20+20+20)  or (11+15+19+20+20+20 ) =100/109/101/105.

THe only possible case to contain 124 pencils is by considering the case : (24+100 ) = (5, 6,6,7, 11+15+15+19+20+20) = 124 .

Hence box 17 - 20 must contain (20, 29, 31, 33).

Option B: Boxes 17 - 20 contain a total of 108 pencils. Since 29, 31, 33 pencils must be a part of 17 - 20 boxes. The remaining box must contain 108 - (29 +31+33) = 15 pencils. Hence the order is (15, 29, 31, 33).

Option C: Boxes 11- 16 contain a total of 101 defective pencils. This is only possible if the boxes here contain : ( 20, 20, 20, 15, 15, 11) pencils. Hence the box containing 19 pencils must be a part of boxes 17 - 20 and the remaining three contain 29, 31, 33. (19, 29, 31, 33)

Option D : Box number 17 containing more pencils than any box from box number 1- 14. Hence this only possible if Box 15, 16, 17 contains 20 pencils each and 18, 19, 20 contain (29, 31, 33).

Option E : Box 7-16 containing 133 broken pencils :

Boxes (1-6) has 6 boxes with broken pencils which can be included from :

(5, 6, 6, 7, 7, 7, 7, 9, 9, 9). The minimum possible sum of the 6 pencils is : (5+6+6+7) = 24 and the maximum possible sum is (7+9+9+9) = 34.

Boxes 7 - 16 contains all the boxes with broken pencils except one among the boxes with broken pencils among 11 - 20 and hence ;

This can contain : (11+15+15+19+20+20) or (15+15+19+20+20+20) or (11+15+15+20+20+20) or (11+15+19+20+20+20 ) =100/109/101/105.

This has multiple possibilities which include (109 + 24) or (101+32) or (105+28). Hence cannot be uniquely determined